Find point inside simple polygon (closed loop), part one
Alec Jacobson
August 06, 2010
I did some pondering today of how to construct an algorithm that given a piecewise linear representation of a simple polygon (a closed loop of points) in 2D return a point that is inside it. It can't be on the boundary or outside, and the algorithm must work for convex and concave polygons. I came up with one solution that I'll post tomorrow. I thought about it throughout the day and had an interesting discussion at lunch at work. Most other algorithms suggested at the table were "quick and dirty" style, usually relying on iterating over a tiny epsilon value. For example: pick some edge on the polygon and check if a tiny distance away from the midpoint on either side is interior, if not then decimate your tiny distance and repeat. These sorts of algorithms didn't have the "cuteness" factor. As a friend at the table put it, "the kind of algorithms that would not make you algorithms professor proud."
At home tonight I searched around on the web and
the first algorithm I found did seem to have the cuteness factor. But at close inspection I noticed that the algorithm as posted is broken. The algorithm goes as quoted:
Given a simple polygon, find some point inside it.
Here is a method based on the proof that there
exists an internal diagonal, in [O'Rourke, 13-14].
The idea is that the midpoint of a diagonal is
interior to the polygon.
1. Identify a convex vertex v; let its adjacent vertices be a and b.
2. For each other vertex q do:
2a. If q is inside avb, compute distance to v (orthogonal to ab).
2b. Save point q if distance is a new min.
3. If no point is inside, return midpoint of ab, or centroid of avb.
4. Else if some point inside, qv is internal: return its midpoint.
So here is my counter example:
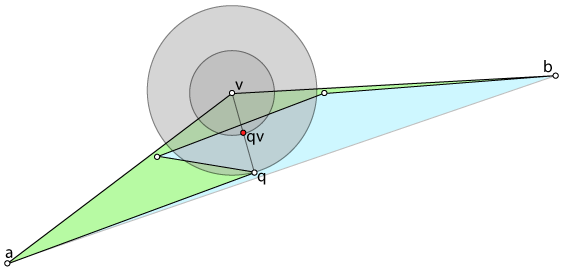If we pick the convex vertex v as marked on the simple polygon in green above, then its adjacent vertices a,b form the blue shaded triangle. The closest other vertex is q, and note that it is indeed with the triangle v->a->b. Now notice that the other two vertices cut an edge not only in between q and v, but even before the midpoint of q->v. Thus the above algorithm terminates having chosen qv, which clearly lies outside the green polygon.
Update:
I could think of a few ways to "fix" this algorithm. But maybe the problem, is just more careful reading (or more careful writing). The algorithm says "compute distance to v (orthogonal to ab)." If you take this to mean: "project v onto the line form by q orthogonal to ab, then compute the distance from this point to q" then I think the algorithm will work OK. With this interpretation/clarification, I'm satisfied that the algorithm is not breakable, though I'm not prepared to prove it.