Common mesh energies, sum notation and matrix notation
Alec Jacobson
June 20, 2011
I'm always re-deriving the matrix notation of common triangle mesh energies like the Dirichlet energy, Laplacian energy, or local rigidity energy. Here's my usual strategy. I'll assume that if your energy came from a continuous integral you can at least get it to a sum over mesh elements. Here I write my sums over vertices and their neighbors, but surely you could also sum over triangles.
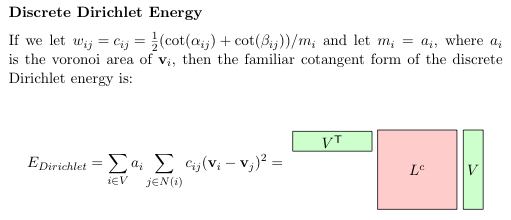 Pretty-printed pdf document
Uglier plain text, unicode version:
Pretty-printed pdf document
Uglier plain text, unicode version:
∑i∑j∈N(i) vi = ∑i * #N(i) * v = VT * D * 1,
where D is diagonal with Dii = #N(i)
∑i∑j∈N(i) vj = VT * A * 1, where A is the adjacency matrix
∑i∑j∈N(i) vi - vj = VT * D * 1 - VT * A * 1 = VT * (D-A) * 1
∑i∑j∈N(i) wij = 1 * Aw * 1, where Aw adjacency with Awij = wij, if j∈N(i)
∑i∑j∈N(i) wij*vi = ∑i vi * ∑j∈N(i) wij = VT * Dw * 1,
where Dw diagonal with Dwii = ∑j∈N(i) wij
∑i∑j∈N(i) wij*vj = VT * Aw * 1
∑i mi * ∑j∈N(i) wij vi = ∑i mi * vi * ∑j∈N(i) wij = VT * M * Dw * 1,
where M is diagonal with Mii = wi
∑i mi * ∑j∈N(i) wij vj = VT * Aw * M * 1
∑i∑j∈N(i) vi² = VT * D * V
∑i∑j∈N(i) vivj = VT * A * V
∑i∑j∈N(i) vj² = VT * RD * V, where RD is diagonal, RDjj = ∑i 1 if j∈N(i)
if j∈N(i) implies i∈N(j) then
D = RD
so ∑i∑j∈N(i) vj² = ∑i∑j∈N(i) vi² = VT * D * V
∑i∑j∈N(i) (vi - vj)² = ∑i∑j∈N(i) vi² - 2 * ∑i∑j∈N(i) vivj + ∑i∑j∈N(i) vj²
= 2 * ∑i∑j∈N(i) vi² - 2 * ∑i∑j∈N(i) vivj
= 2 * VT * D * V - 2 * VT * A * V
= 2 * VT * (D - A) * V
= 2 * VT * L * V
∑i∑j∈N(i) wij*vi² = ∑i vi² * ∑j∈N(i) wij = VT * Dw * V
∑i∑j∈N(i) wij*vivj = VT * Aw * V
∑i∑j∈N(i) wij*vj² = VT * RDw * V, where DW is diagonal, RDwjj = ∑i wij if j∈N(i)
if j∈N(i) implies i∈N(j) and wij = wji then
Dw = RDw
so ∑i∑j∈N(i) wij*vj² = ∑i∑j∈N(i) wij*vi² = VT * Dw * V
∑i∑j∈N(i) wij(vi - vj)² =
= ∑i∑j∈N(i) wij*vi² - 2 * ∑i∑j∈N(i) wij*vivj + ∑i∑j∈N(i) wij*vj²
= 2 * ∑i∑j∈N(i) wij*vi² - 2 * ∑i∑j∈N(i) wij*vivj
= 2 * VT * Dw * V - 2 * VT * Aw * V
= 2 * VT * (Dw - Aw) * V
= 2 * VT * Lw * V
∑i mi * ∑j∈N(i) wij vi² = ∑i mi * vi² * ∑j∈N(i) wij = VT * M * Dw * V
∑i mi * ∑j∈N(i) wij vj² = VT * RDw * M * V
∑i mi * ∑j∈N(i) wij vivj = VT * Aw * M * V
∑i mi * ∑j∈N(i) wij(vi - vj)² =
= ∑i mi * ∑j∈N(i) wij*vi²
- 2 * ∑i mi * ∑j∈N(i) wij*vivj
+ ∑i mi *∑j∈N(i) wij*vj²
= 2 * ∑i mi * ∑j∈N(i) wij*vi² - 2 * ∑i mi * ∑j∈N(i) wij*vivj
= 2 * VT * M * Dw * V - 2 * VT * Aw * M * V
= 2 * VT * M * (Dw - Aw) * V
= 2 * VT * M * Lw * V
Note: let wij = cwij = cot(αij) + cot(βij) / mi and let mi = voronoi area at
vi, then the familar cotangent form of the discrete Dirichlet energy is
EDirichlet = 2 * VT * M * Lcw * V
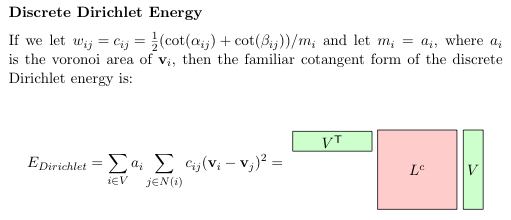 Pretty-printed pdf document
Uglier plain text, unicode version:
Pretty-printed pdf document
Uglier plain text, unicode version: