Bijective mappings with generalized barycentric coordinates: a counterexample

Alec Jacobson

December 11, 2012

weblog/

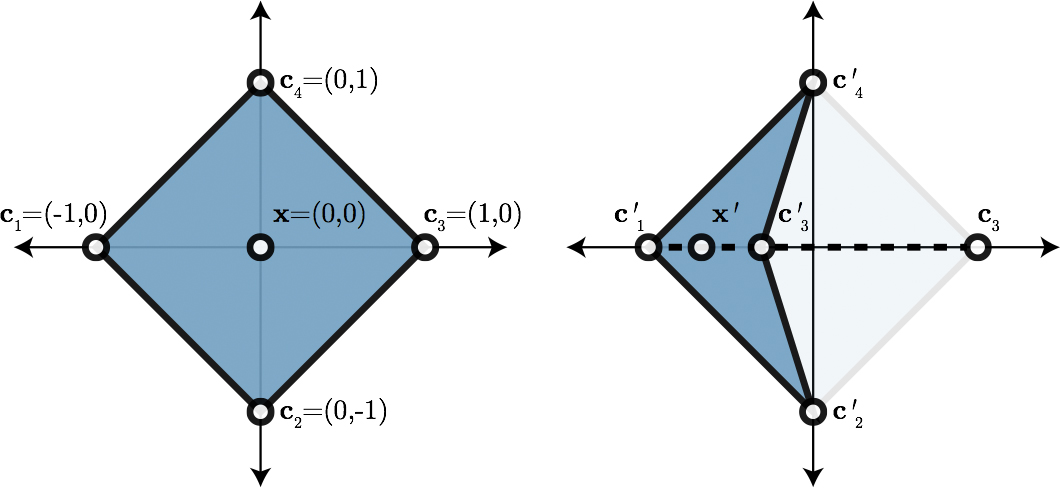
bijective barycentric coordinates: counter example After attending the NFS Workshop on Barycentric Coordinates this summer I wrote up a quick counterexample showing that generalized barycentric coordinates cannot be designed to always produce bijective mappings. To be clear, no existing coordinates have claimed to obtain this property, but as far as I know no one has written explicitly that it's out of reach. Abstract Many recent works attempt to generalize barycentric coordinates to arbitrary polygons. I construct a counterexample proving that no such generalization will produce purely bijective mappings in the plane provided the coordinates meet the Lagrange, reproduction, and partition of unity properties. The proof concerns generalized barycentric coordinates in a square, but trivially generalizes to arbitrary polygons with degree greater than three. Sketch Consider the four corners of square above. As we move c3 towards c1 the point x originally at the origin will either:
  1. be overrun by c3 before c3=c1 (not bijective),
  2. reach (and thus overrun) c1 before c3=c1 (not bijective)
  3. or the coordinate function of w3(x)=0.5 (bijective)
But by rotational symmetry we may apply the same logic for all 4 corners implying that to get a bijection we have all four coordinates =0.5 contradicting the partition of unity assumption.