How often is the championship loser the second best team?

Alec Jacobson

January 02, 2025

weblog/

TL;DR More often than not.

The new year leads into a bunch of playoff seasons in North American sports. Seeing the visualizations of playoff brackets got me wondering how often the team that loses in the championship game ("silver medalist") is the second best team in the tournament. Maybe the second best team was actually eliminated by the best team earlier in their bracket. It makes it seem that all we really know about the championship loser is that they're better than their own bracket: or only 50% of the teams. That's not very impressive! Or can we say more?

To make things mathematically tidy, let's assume a "sport" where two competing teams simpler compare their preordained ranking. The better ranking wins. So if $n$ is a power of two, and $n$ teams compete in simple single-elimination bracket style playoff where teams are uniformly randomly assigned into initial bracket positions.

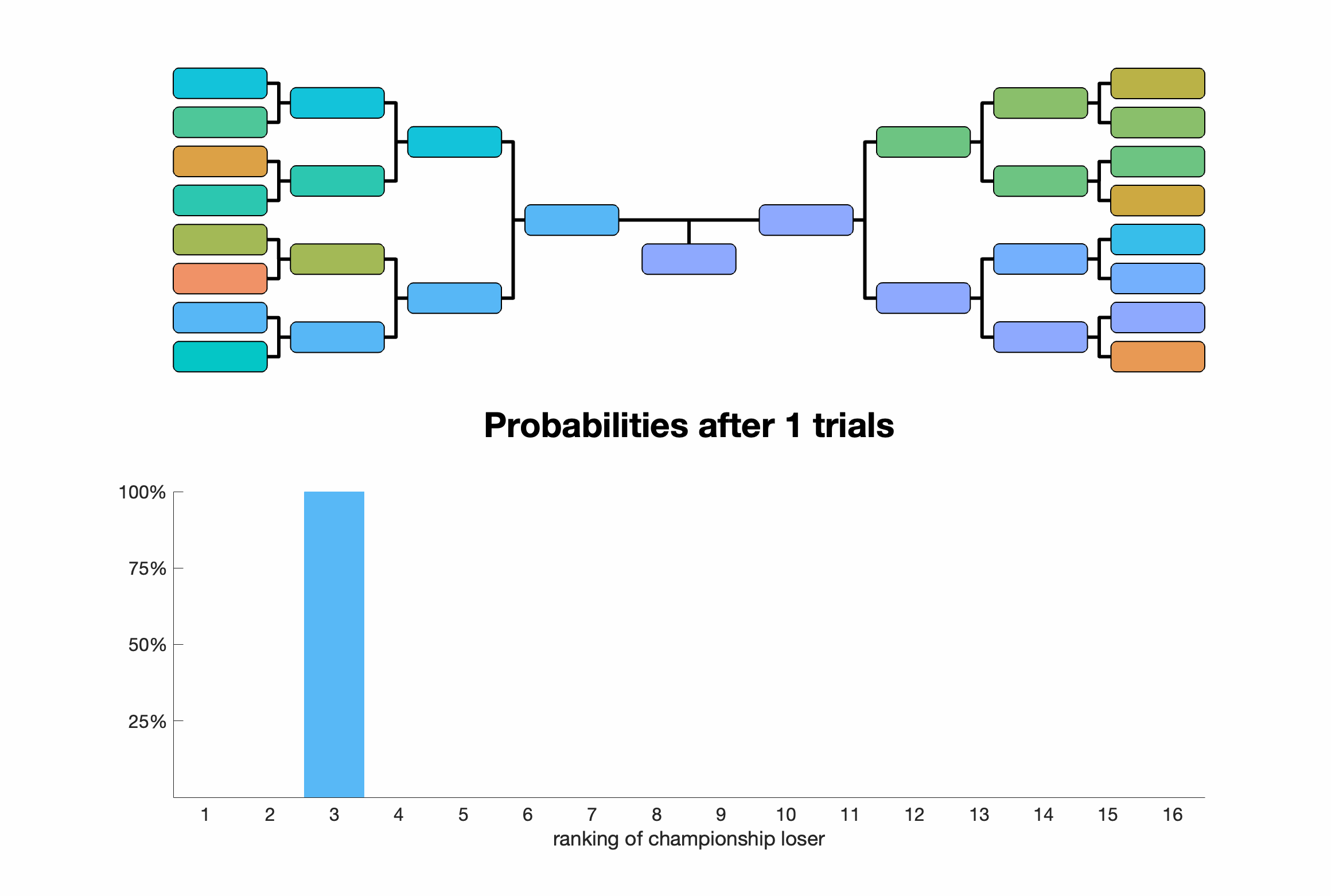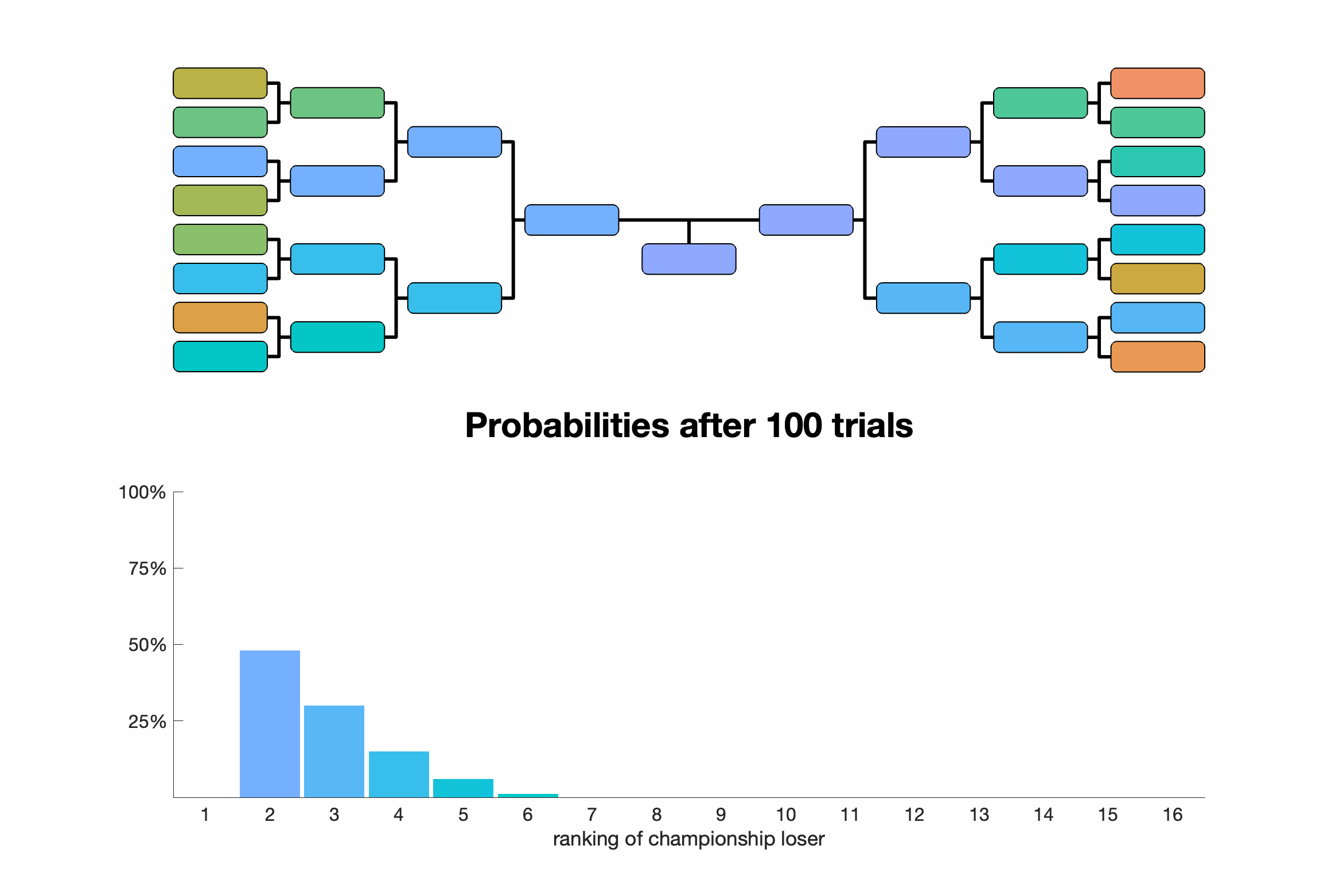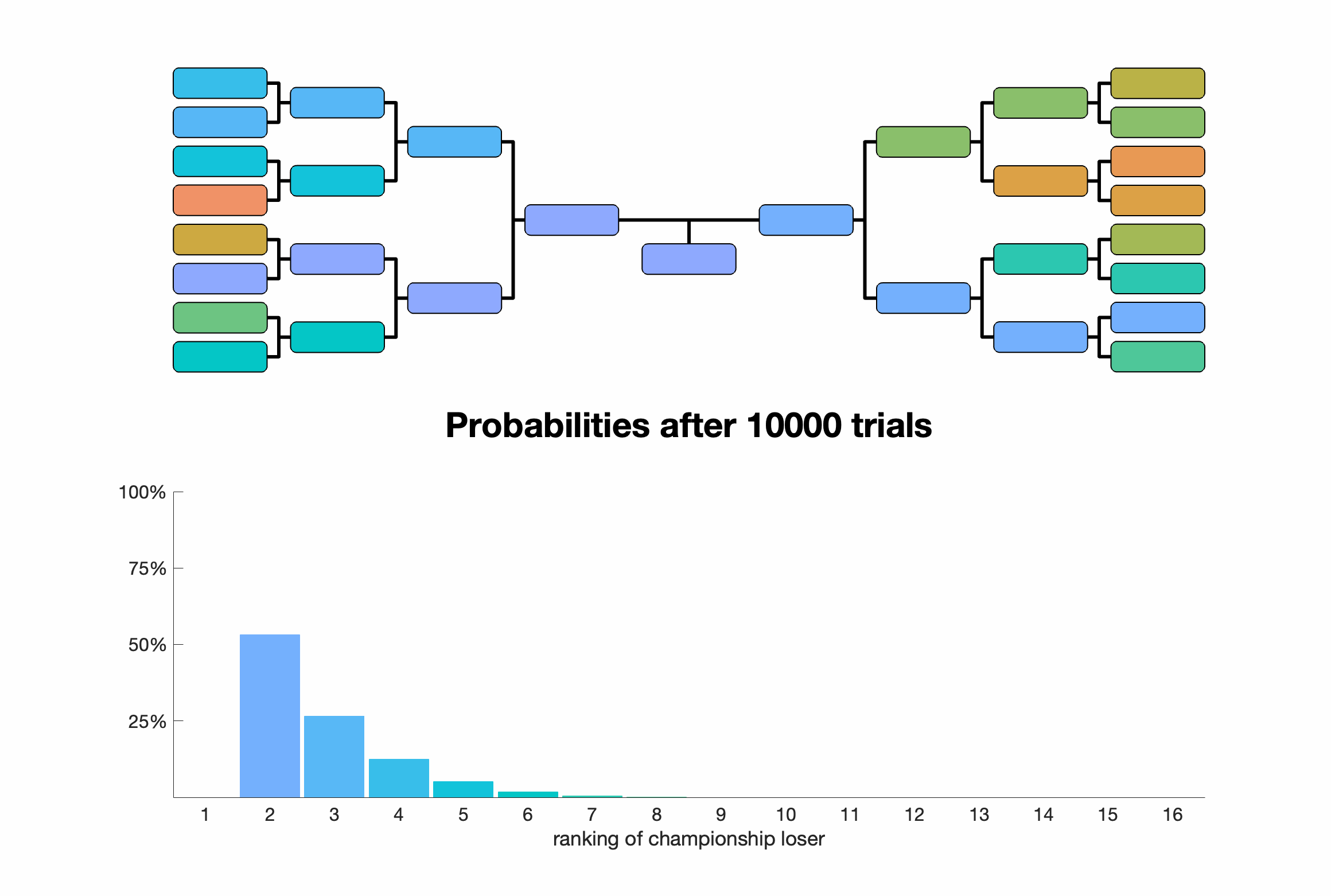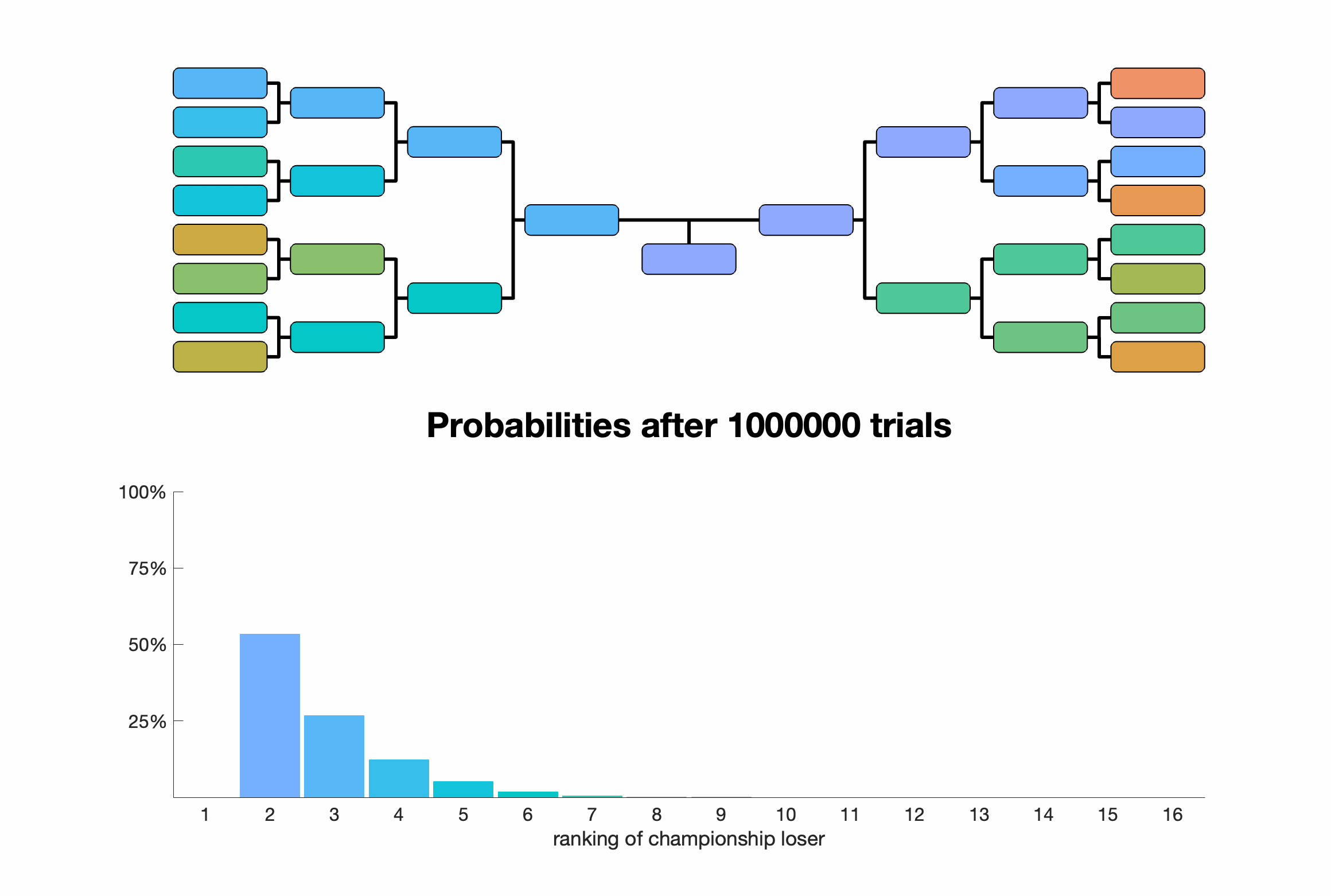
The championship is, of course, the match between best ranked teams from the two halves of the bracket (each containing $n/2$ teams). By our simple "sport", the winner of the championship trivially has the best ranking ($1$). The loser of the championship could have any ranking between $2$ and $n/2+1$ (inclusive). Our question is: what is the probability that the loser of the championship has ranking $r=2$? Or more generally, what's the probability distribution over the rankings of the championship loser?

Fine, but in the NFL, NCAA, PWHL, NHL, NBA, etc. the $n$ is usually quite small. Sometimes, $n=8$ or even $n=4$. The limit case formula is bad for small $n$ because 1) it doesn't produce $p(r \ge n/2+2)=0$ and 2) it's quite far off in value for others. For example, for $n=4$ you can just enumerate all possibilities and see that: \begin{align} p_{n=4}(r=2) &= 2/3 \\ p_{n=4}(r=3) &= 1/3 \\ p_{n=4}(r=4) &= 0, \end{align} which clearly doesn't match the limit case formula.

Keeping $n$ finite, if we only care about whether the championship loser was the second best team then we consider which half of the bracket the second best team ends up in. There are $n-1$ slots left over after the first team is placed, of those there are $n/2$ in the bracket that the first place team is not in, and hence would result in a championship game between the two. So the probability is: \[ p_{n}(r=2) = \frac{n/2}{n-1}. \]

More generally if we want to know the probability that the championship loser has ranking $r=d$ then we can compute an accurate formula by: Looking for all permutations of the values ${1,2,\dots,n}$ such that $d$ is the smallest value in the one half of the permutation. There are $\begin{pmatrix} n-1 \\ n/2-1 \end{pmatrix}$ ways to choose the other $n/2-1$ elements in the half containing the value $1$. For $d$ to be the smallest value in the other half, then all values $\{2,\dots,d-1\}$ must be in the half containing $1$. We now just need to know how many ways there are to arrange the remaining values. With $n-d$ slots left, we choose $n/2-d+1$ of them to ensure that $d$ ends up the smallest value in the other half. Thus our formula is: \[ p_{n}(r=d) = \frac{ \begin{pmatrix} n-d \\ n/2+1-d \end{pmatrix}} {\begin{pmatrix} n-1 \\ n/2-1 \end{pmatrix}} \].

And indeed the limit as $n$ increases gives the simple formula we above: \[ \lim_{n\rightarrow\infty} p_{n}(r=d) = \lim_{n\rightarrow\infty} \frac{ \begin{pmatrix} n-d \\ n/2+1-d \end{pmatrix}} {\begin{pmatrix} n-1 \\ n/2-1 \end{pmatrix}} = 2^{1-d}. \]

For $n=8$, the championship loser has a ranking of $r$ with probabilities: \begin{align*} p_{n=8}(r=2) &\approx 0.571 \\ p_{n=8}(r=3) &\approx 0.286 \\ p_{n=8}(r=4) &\approx 0.114 \\ p_{n=8}(r=5) &\approx 0.029 \\ p_{n=8}(r\ge 6) &= 0. \end{align*}

For $n=16$, the championship loser has a ranking of $r$ with probabilities: \begin{align*} p_{n=16}(r=2) &\approx 0.5333 \\ p_{n=16}(r=3) &\approx 0.2667 \\ p_{n=16}(r=4) &\approx 0.1231 \\ p_{n=16}(r=5) &\approx 0.0513 \\ p_{n=16}(r=6) &\approx 0.0186 \\ p_{n=16}(r=7) &\approx 0.0056 \\ p_{n=16}(r=8) &\approx 0.0012 \\ p_{n=16}(r=9) &\approx 0.0002 \\ p_{n=16}(r\ge 10) &= 0. \end{align*}

In our simulated playoffs, the championship loser is the second best team non-trivially more often than not. In real playoffs, there's often a seeding and biased ordering system which surely would affect these probabilities. Bracket halves also often correspond to geographic or other non-uniformly random splits of the competitors. Most sports don't deterministically rely on a single transitively sortable attribute; accounting for that makes the dynamics much more interesting and difficult.

As a tangent, this problem appears to be a reasonably good test question for large language models. In the end, it's a undergrad Combinatorics quiz question so not research level math, but nonetheless appears to trip up many of the models. Here's my tally:

Model	Response
ChatGPT o1	✅ (not simplified)
ChatGPT 4o	❌ (only limit case)
ChatGPT 4	✅
Gemini 1.5	❌
Github Copilot in .py	❌
Copilot	❌ (only limit case)
Claude 1.5 Sonnet	❌

And here's my prompt:

Let's say we're given a number n, which is a clean power of two (n = 2^p) for an integer p≥1. Now consider a random permutation of the integers 1..n. Call this sequence R. Split the sequence into two halves: R₁ and R₂. One of the halves will contain the minimum value (1), call that Rᵢ. Consider the minimum value in the other half: r = min( Rⱼ)  where j ≠ i. Sometimes this minimum value will be 2, but sometimes the 2 value will be in the same half as the minimum over all (2 ∈ Rᵢ). Similar for 3 and so on until the value of n/2+1 which has no chance of being the minimum in the other half (since worst case all 1...n/2 lie in one half, leaving at least n/2-1 in the other half).

OK so the question for you is what is a formula for the probability of each r value as a function of n and value considered (let's call it d). Do not consider the limit case. Consider finite n as defined above. Specifically:

p(r = d) = [fill in this function of n and d].

Hint: this formula must be

p(r = n/2-2) = 0