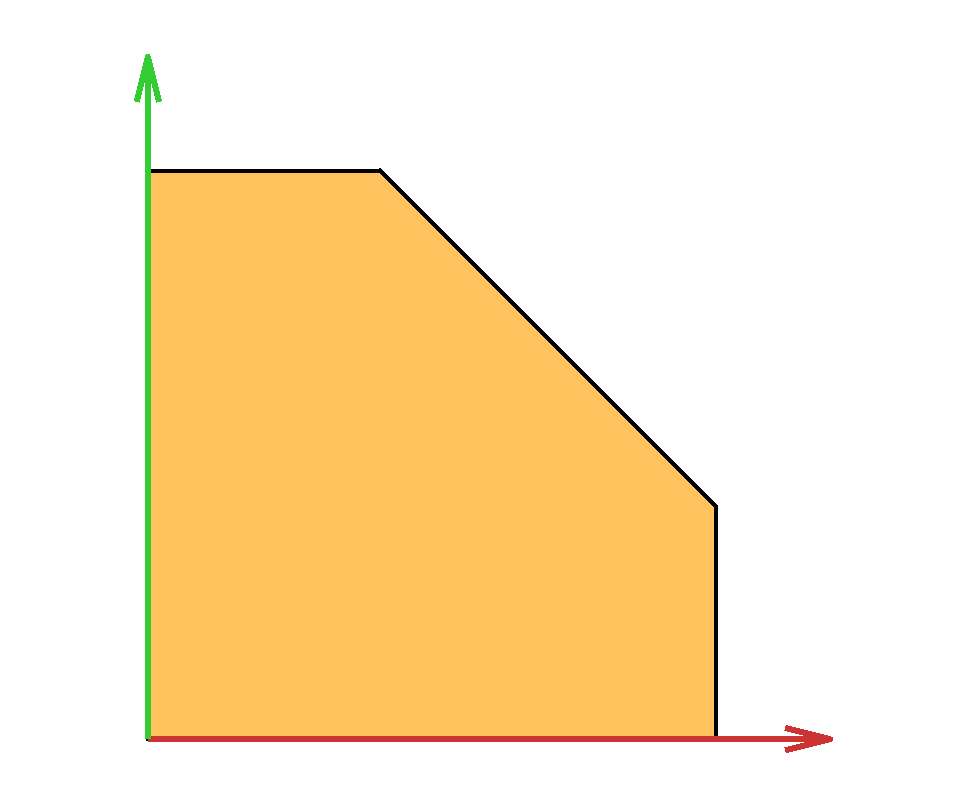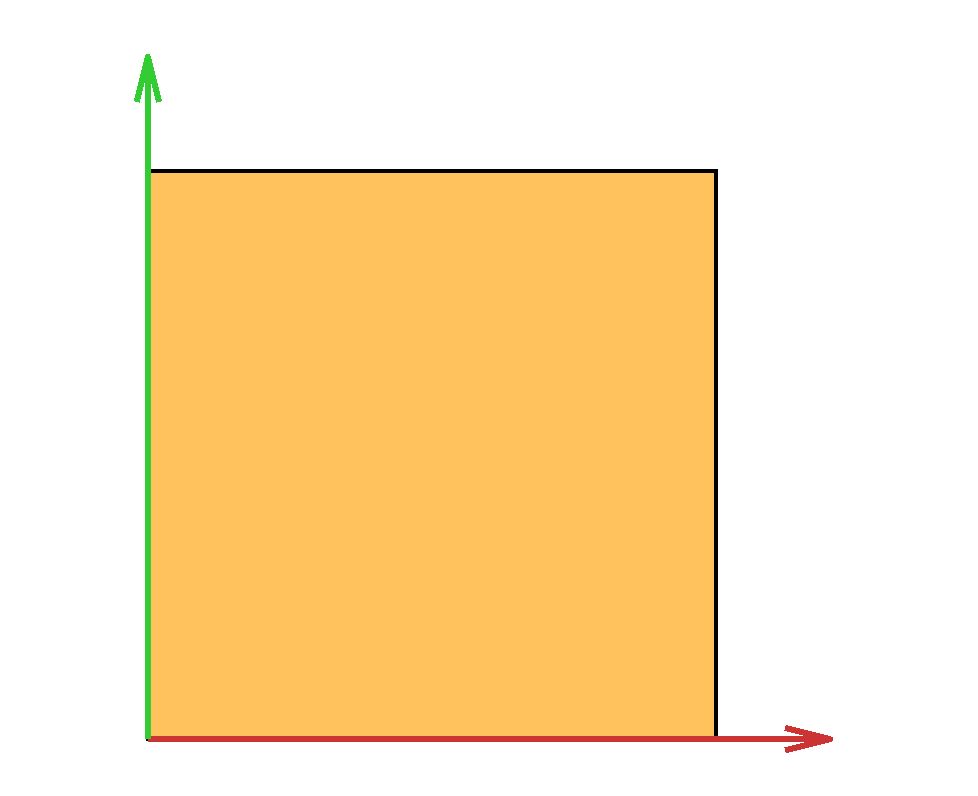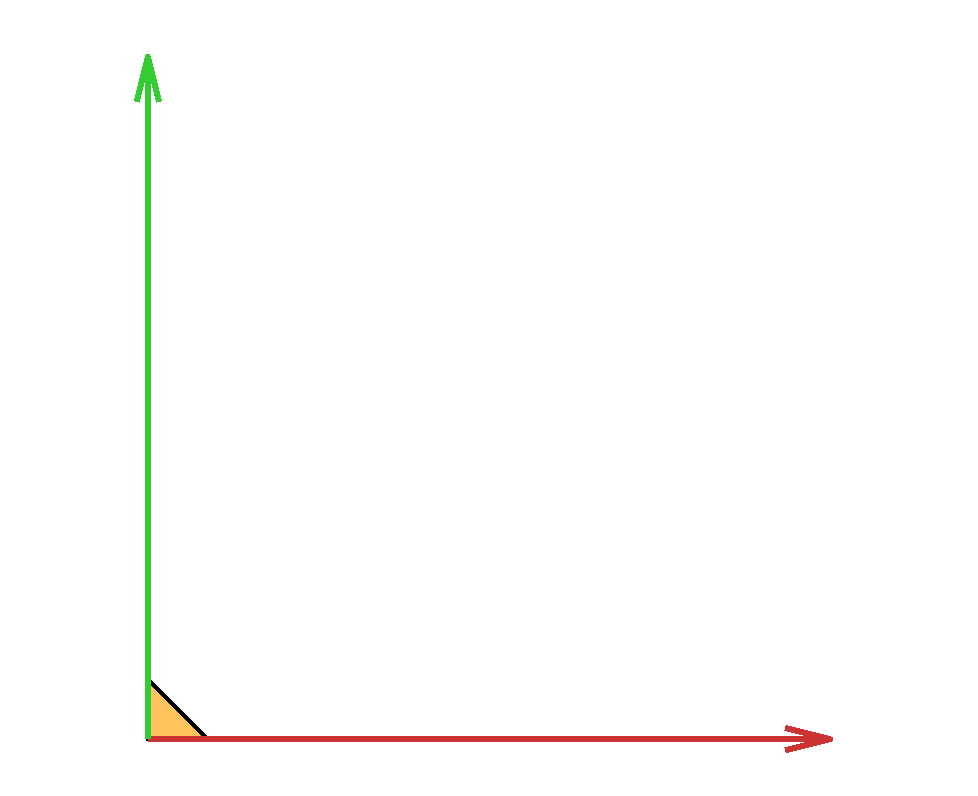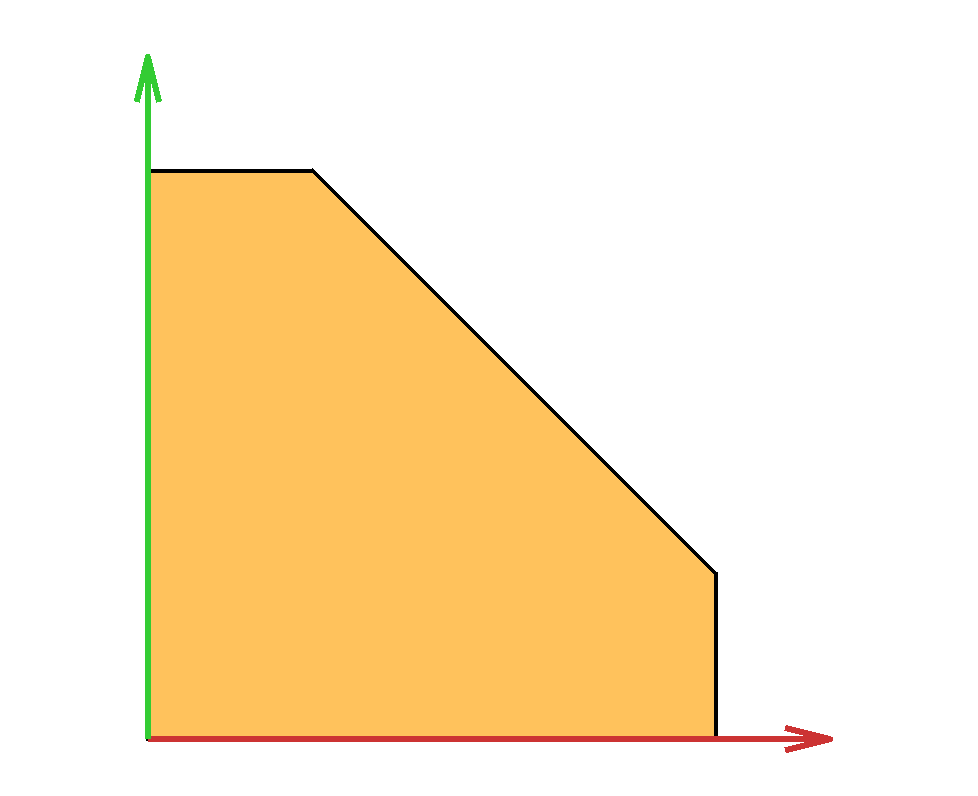
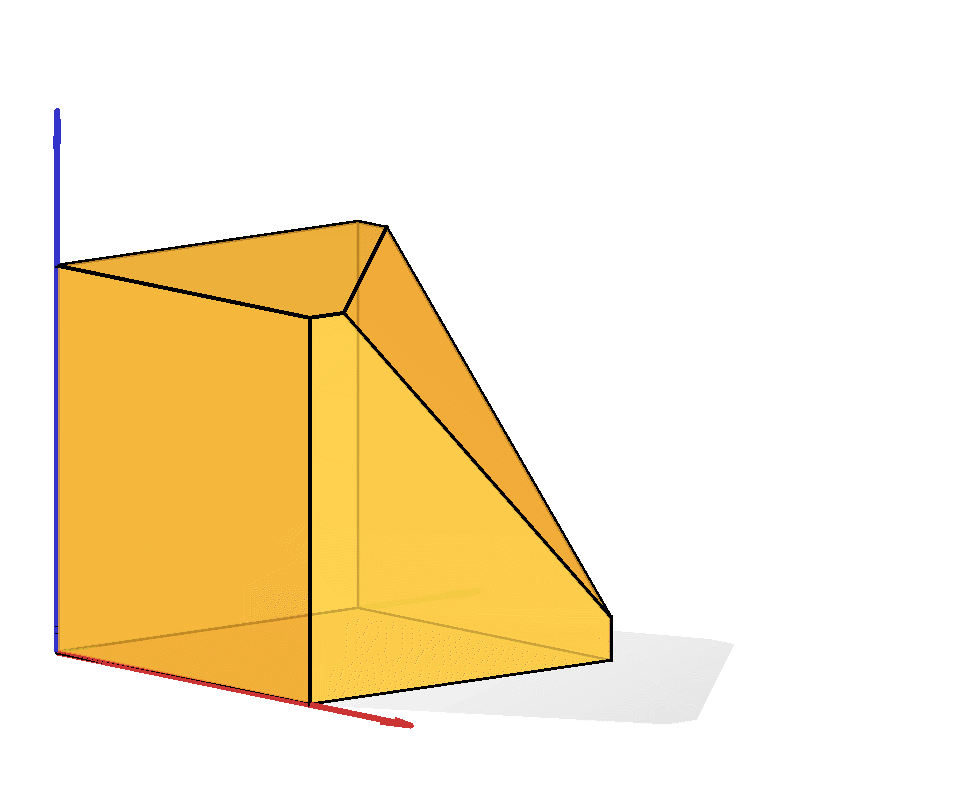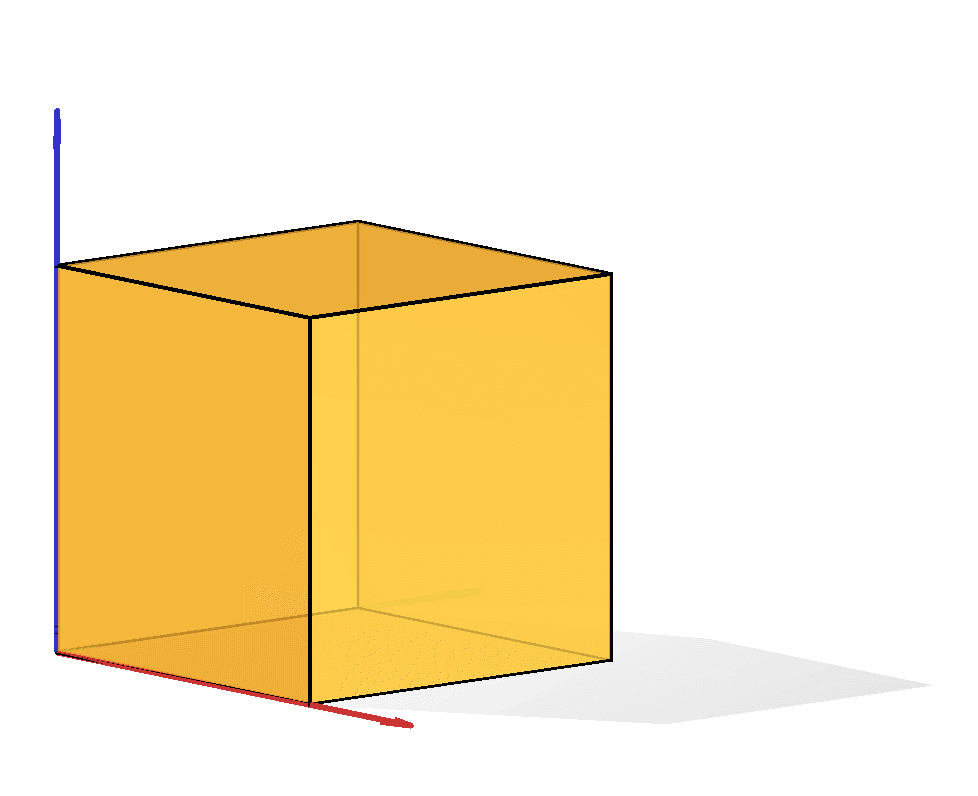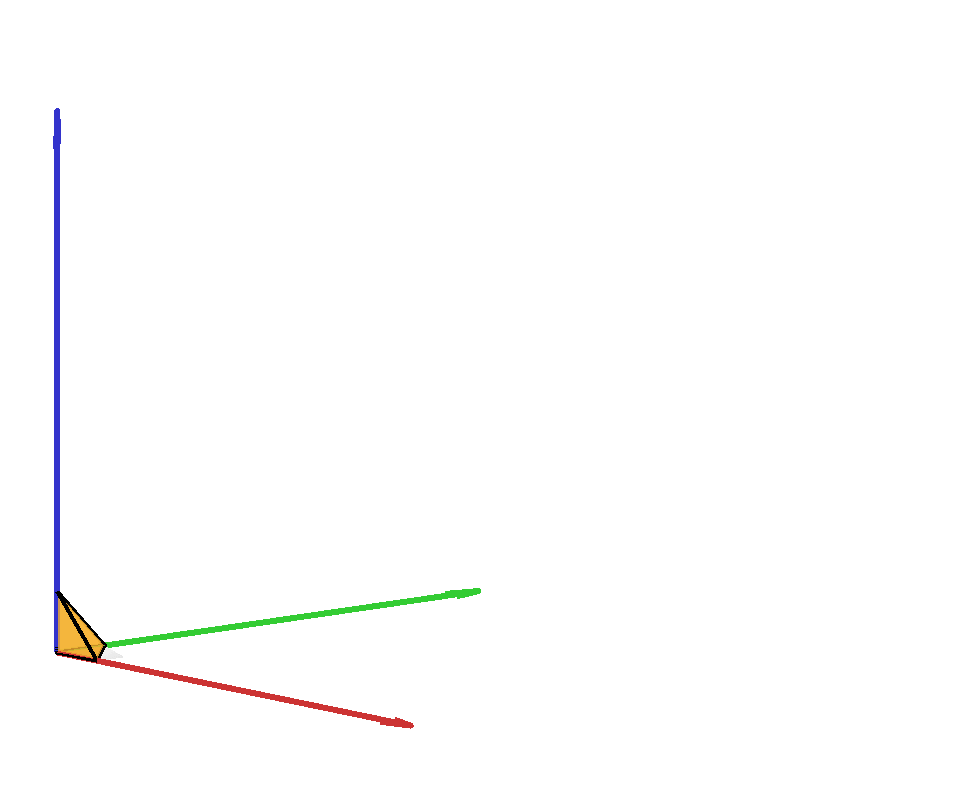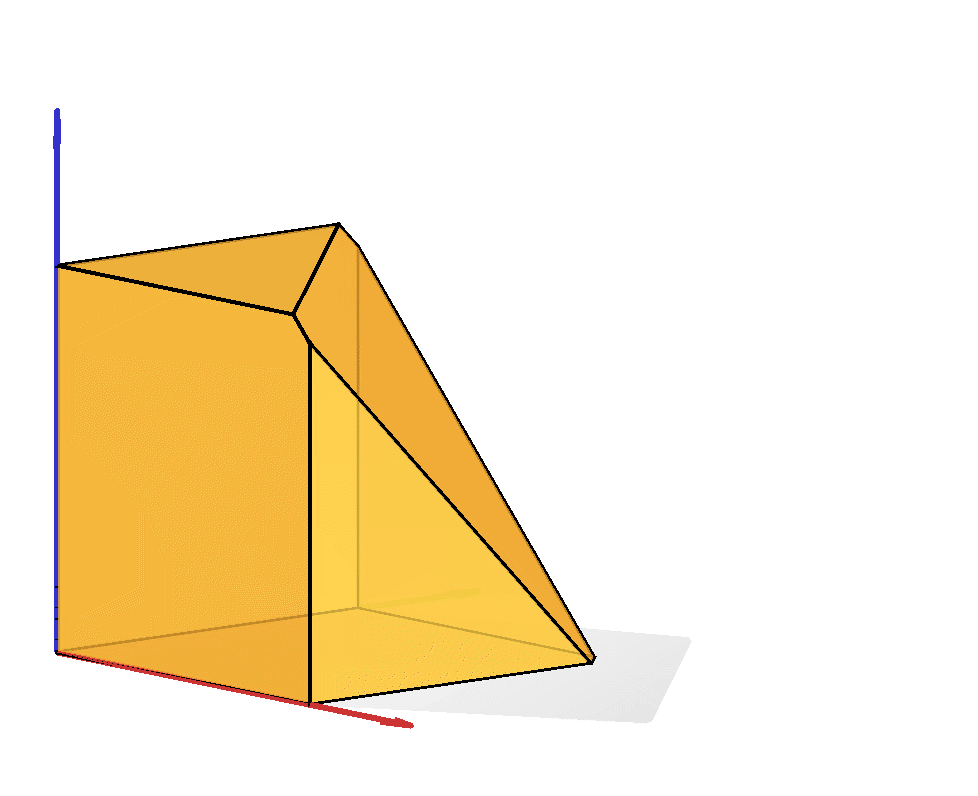
The capped simplex is defined as the set of points in the unit hypercube that sum to less than a given value $s$: $$ \left\{ x \in \mathbb{R}^n \ \middle|\ \sum_{i=1}^n x_i \leq s \text{ and } 0\leq x_i \leq 1\right\}. $$


Sampling from the capped simplex when $n$ is small is trivial and efficient with rejection sampling (e.g., sampling $x \sim [0,1]^n$ and then rejecting if $\sum x_i\gt s$). For large $n$, rejection sampling is quickly intractable. The volume of the capped simplex is given by the formula: $$ C(n,s) = \frac{1}{n!} \sum_{k=0}^{\lfloor s \rfloor} (-1)^k \begin{pmatrix}n\\k\end{pmatrix} (s-k)^n. $$ Consider $n=30$ and $s=5$, the acceptance rate for rejection sampling would be less than $10^{-11}\%$.
A better approach is to sample the simplex scaled by $s$ and then reject points with any coordinate greater than 1. There are various ways to sample that simplex but one is to: $$ u \sim \text{Uniform}\left([0,1]^{n+1} \right) \\ y = -\log(u) \\ x_i = s \frac{y_i}{\sum_{j=1}^{n+1} y_j} \quad \text{for } i=1,\ldots,n. $$ Now we reject if any $x_i \gt 1$.
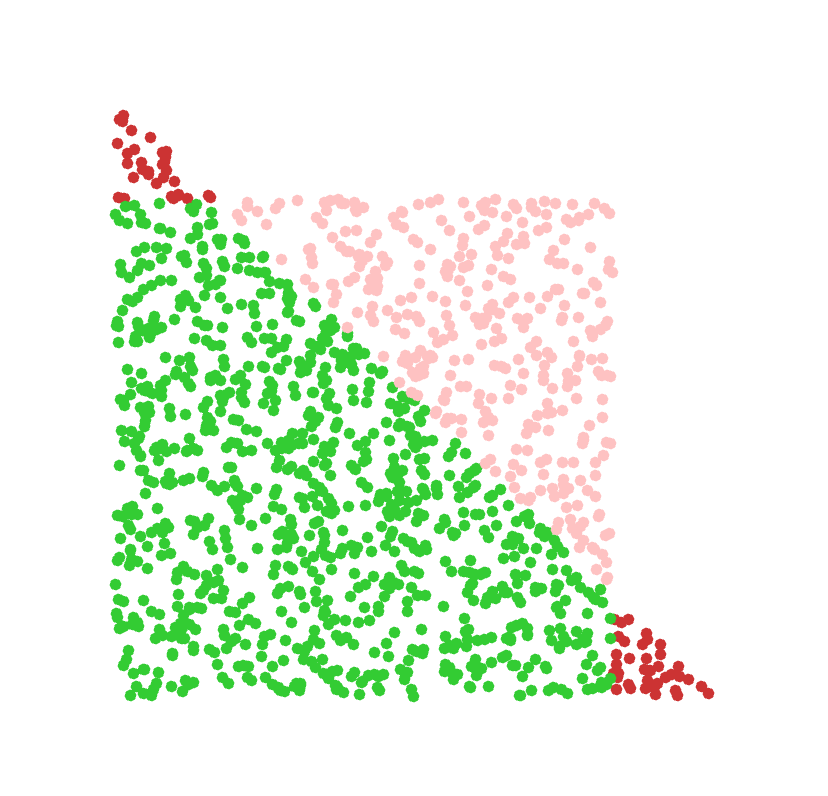
As $n$ grows the volume of the of the $s$-simplex is given by: $$ S(n,s) = \frac{s^n}{n!}. $$ This means the acceptance rate for this method is: $$ \frac{C(n,s)}{S(n,s)} = \sum_{k=0}^{\lfloor s \rfloor} (-1)^k \begin{pmatrix}n\\k\end{pmatrix} \left(1-\frac{k}{s}\right)^n, $$ which goes to $1$ as $n$ grows with fixed $s$: basically free!
For fixed $n$, there's a crossover point as $s$ grows when the acceptance rate becomes better to just use the hypercube again. This happens when: $$ s \ge (n!)^{1/n}. $$ But that's not super useful for large $n$ as it also tends toward 0, so for moderate $s$ relative to large $n$ we're not accepting many samples in either method.
ChatGPT helped derive a more direct method that does not rely on rejection sampling. Suppose $x$ was drawn uniformly from the $s$-capped simplex in $\mathbb{R}^n$ and consider the first coordinate $x_1=t$. Conditioned on $x_1=t$, the remaining coordinates $(x_2,\dots,x_n)$ are uniform on the $(s-t)$-capped simplex in $\mathbb{R}^{n-1}$. Therefore the marginal density of $x_1$ is proportional to the remaining feasible volume: $$ p_{x_1}(t) = \frac{C(n-1,s-t)}{C(n,s)}, \qquad 0 \le t \le \min(1,s). $$ Integrating gives the cumulative distribution function: $$ F_{x_1}(t) = \frac{1}{C(n,s)}\int_0^t C(n-1,s-u)\,du. $$
We can sample $x_1$ by drawing $r_1\sim\mathrm{Uniform}\left([0,1]\right)$ and solving for $t$ such that $F_{x_1}(t)=r_1$ via bisection root finding. Then we recurse on dimension $n-1$ with updated cap $s\leftarrow s-x_1$ to sample $x_2$, and so on. This produces uniform samples from the $s$-capped simplex without any rejection.
For double precision, bisection probably needs 50-ish iterations to get maximum accuracy. So it's not super cheap, but still may be worth it some situations. For example, when $n=150$ and $s=56$, the rejection sampling methods both have acceptance rates of about $10^{-5}\%$.
The other reason we might like this recursive direct sampling method is to use it as a parameterization over the capped simplex. If we keep (or recover) the random seeds $r_i$ used to generate each of the coordinates, this gives a mapping from $[0,1]^n$ to the capped simplex. We can differentiate this (skipping the bisection steps) to get jacobian matrices with respect to the random seeds: $\partial x / \partial r$. I'm not going to bother working this out because it's probably best for autodiff or symbolic differentiation to handle it anyway. The mapping is of course only piecewise smooth due to the corners of the capped simplex, but this seems inevitable unless we give up uniformity.